HashMap 详解五

发表于

红黑树性质

  1. 红黑树是平衡二叉树的一种, 但是它的平衡因子是可以大于 1
  2. 红黑树的节点要么是红色, 要么是黑色, 这里的红黑色只是用来区分的一种方式, 为了定义规则
  3. 根节点一定是黑色
  4. 叶子节点也是黑色, 实际上叶子节点都是由 NULL 组成
  5. 红色节点的子节点是黑色
  6. 根节点到叶子节点的路径都包含相同数量的黑色节点

红黑树与 AVL 树的区别

红黑树在线模拟链接: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
AVL 树在线模拟链接: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
依次插入: 1, 2, 3, 4, 5, 6, 红黑树会出现左右子树高度差大于 1 的情况, AVL 树就不会, 平衡因子不会超过 1, 最终结果如下:
红黑树: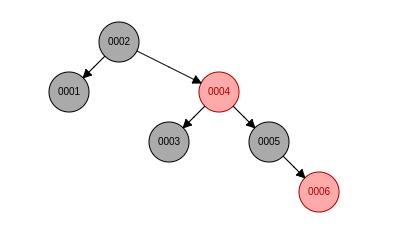

AVL 树: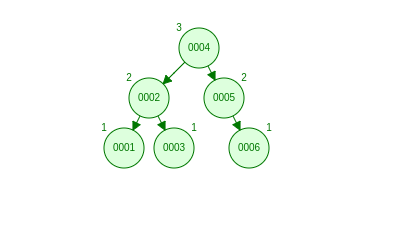

红黑树插入

  1. 节点只有红黑两种颜色, 假设插入节点是黑色, 那么会导致这条路径的黑色节点比其他路径要长, 违反性质 6, 所以新节点要为红色;
  2. 如果是根节点, 变成黑色, 接下来的操作分两种情况, 一种是父节点是黑色, 简称黑父; 另一种父节点是红色, 简称红父;
  3. 黑父, 插入红节点满足性质, 什么都不用做;
  4. 红父, 这个情况又要分为两种情况, 一是红叔, 一是黑叔;
    1) 红叔
    将父叔节点变成黑色, 为了不违反性质 6, 祖父节点就变成红色; 当祖父节点变成红色, 相当于插入一个新节点到祖父节点的位置, 这时候需要继续向上迭代, 重新走插入流程
    2) 黑叔
    这个情况就复杂多了, 不仅要改变节点颜色, 还要进行旋转, 具体可以分为 4 种情况:
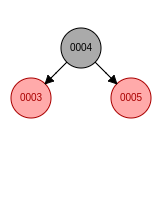
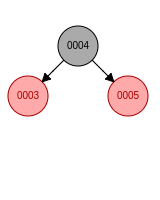
    a. 新节点位于祖父节点的左孩子的左子树, 先右旋, 父节点变成黑色, 祖父节点变成红色
    b. 新节点位于祖父节点的左孩子的右子树, 先左旋再右旋, 新节点变成黑色, 祖父节点变成红色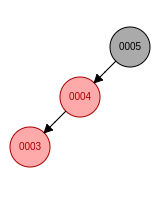
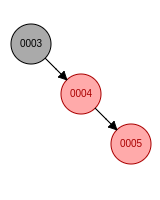
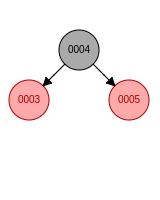    c. 新节点位于祖父节点的右孩子的右子树, 先左旋, 父节点变成黑色, 祖父节点变成红色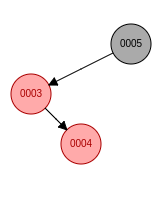
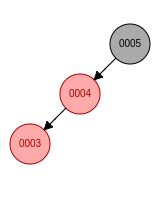
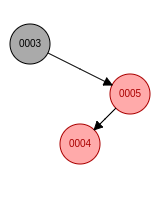
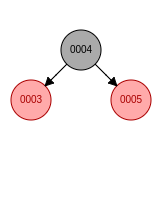    d. 新节点位于祖父节点的右孩子的左子树, 先右旋再左旋, 新节点变成黑色, 祖父节点变成红色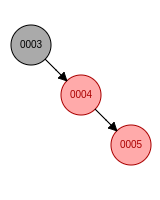

putTreeVal()

HashMap 中如果是树结构, 那么使用的是红黑树结构, 因为查询的时间复杂度都是 O(logN), 而保存键值对是通过 putTreeVal 方法, 这里可以看上一 part. 这个方法并不是 HashMap 的方法, 而是 HashMap 的内部类 TreeNode 的方法, 这个内部类用来表示树节点, 包含几个属性: parent, left, right, prev, next, red.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
// 返回树的根节点
final TreeNode<K,V> root() {
    for (TreeNode<K,V> r = this, p;;) {
        if ((p = r.parent) == null)
            return r;
        r = p;
    }
}

/**
 * 如果树存在相同 key 的节点, 那么会直接返回这个节点; 如果没有就插入新节点
 * map: 表示 HashMap 本身
 * tab: 表示数组
 * h: 表示 key 的哈希值
 * k: 表示 key
 * v: 表示 value
 */
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                                       int h, K k, V v) {
    Class<?> kc = null;
    boolean searched = false;

    // 获取根节点
    TreeNode<K,V> root = (parent != null) ? root() : this;

    // 遍历树, p 表示当前节点
    for (TreeNode<K,V> p = root;;) {

    	// dir: -1 表示向左遍历, 1 表示向右遍历
    	// ph: 表示当前节点的 key 的哈希值
    	// pk: 表示当前节点的 key
        int dir, ph; K pk;

        // 新节点的哈希值小于当前节点, 向左遍历, dir 设置为 -1
        if ((ph = p.hash) > h)
            dir = -1;
        // 新节点的哈希值大于当前节点, 向右遍历, dir 设置为 1
        else if (ph < h)
            dir = 1;
        // 新节点的 key 和当前节点相同, 直接返回当前节点
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
        // 新节点的哈希值和当前节点的哈希值相同, 但是 key 不相同
        // comparableClassFor 方法会返回实现 Comparable 接口的类型, 否则返回空
        // compareComparables 方法会返回 k 与 pk 比较后的值
        // 也就是说这里是处理当前节点没有实现 Comparable 接口
        // 或者新节点通过 Comparable 接口比较后还是相等的情况
        else if ((kc == null &&
                  (kc = comparableClassFor(k)) == null) ||
                 (dir = compareComparables(kc, k, pk)) == 0) {
            // 当前节点的左右子树可能也相同, 所以向下搜索符合哈希值和 key 的节点 
            if (!searched) {
                TreeNode<K,V> q, ch;
                searched = true;
                if (((ch = p.left) != null &&
                     (q = ch.find(h, k, kc)) != null) ||
                    ((ch = p.right) != null &&
                     (q = ch.find(h, k, kc)) != null))
                    return q;
            }
            // 比较哈希值, 小于等于返回 -1, 大于返回 1
            dir = tieBreakOrder(k, pk);
        }

        // 记录当前节点
        TreeNode<K,V> xp = p;
        // 根据 dir 判断左遍历还是右遍历, 子节点为空说明来到了叶子节点, 把新节点插入就可以了
        if ((p = (dir <= 0) ? p.left : p.right) == null) {
            Node<K,V> xpn = xp.next;
            // 新节点, next 指向父节点的 next
            TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);

            // 根据 dir 决定是插入到左子树还是右子树
            if (dir <= 0)
                xp.left = x;
            else
                xp.right = x;

            // 这里设置父子双向链表关系, 把父节点原来的 next 节点的 prev 指向新节点
            xp.next = x;
            x.parent = x.prev = xp;
            if (xpn != null)
                ((TreeNode<K,V>)xpn).prev = x;

            // balanceInsertion() 方法将树修改成符合红黑树性质
            // 树旋转后可能会根节点转掉, 那么数组索引位置对应节点就不是根节点了
            // moveRootToFront() 方法确保索引位置对应根节点
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }
}

balanceInsertion()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
/**
 * root: 根节点
 * x: 新节点
 * 这个方法是把树改成符合红黑树性质的过程, 可以结合上面红黑树插入来看
 */
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                                    TreeNode<K,V> x) {
    // 设置新节点为红色
    x.red = true;

    // xp: 父节点
    // xpp: 祖父节点
    // xppl: 祖父节点左孩子
    // xppr: 祖父节点右孩子
    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
    	// 父节点为空, 说明这是根节点, 设置成黑色
        if ((xp = x.parent) == null) {
            x.red = false;
            return x;
        }
        // 黑父, 什么都不做, 至于还要判断祖父节点是否为空就不知道为什么了
        else if (!xp.red || (xpp = xp.parent) == null)
            return root;

        // 红父, 并且该节点位于祖父节点的左子树
        if (xp == (xppl = xpp.left)) {

            // 红叔, 只要修改颜色即可
            // 红叔变黑叔
            // 红父变黑父
            // 祖父节点变红色
            // 新节点指向祖父节点, 继续向上迭代
            if ((xppr = xpp.right) != null && xppr.red) {
                xppr.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            }

            // 黑叔
            else {
            	// 新节点位于祖父节点的左孩子的右子树, 需要先左旋, 具体方法看下面
            	// 左旋完成后当前节点变成父节点, 原来的父节点变成了当前节点, 这是为下面右旋准备
                if (x == xp.right) {
                    root = rotateLeft(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                // 右旋, 具体方法看下面
                // 父节点(原来新节点)变黑色, 祖父节点变红色
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateRight(root, xpp);
                    }
                }
            }
        }
        
        // 红父, 并且该节点是祖父节点的右子树
        else {

            // 红叔, 只要修改颜色即可, 参考上面
            if (xppl != null && xppl.red) {
                xppl.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            }

            // 黑叔
            else {
            	// 新节点位于祖父节点右孩子的左子树, 需要先右旋
                if (x == xp.left) {
                    root = rotateRight(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                // 然后统一左旋, 处理跟上面一样
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
}

/**
 * 左旋, 实际是通过修改节点的父与子指针来实现
 * root: 根节点
 * p: 新节点的父节点
 */
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                              TreeNode<K,V> p) {
    // r: p 的右孩子
    // pp: p 的父节点
    // rl: p 的右孩子的左孩子
    TreeNode<K,V> r, pp, rl;
    // 过滤参数错误的情况, 判断是否能够进行左旋
    if (p != null && (r = p.right) != null) {
        if ((rl = p.right = r.left) != null)
            rl.parent = p;
        if ((pp = r.parent = p.parent) == null)
            (root = r).red = false;
        else if (pp.left == p)
            pp.left = r;
        else
            pp.right = r;
        r.left = p;
        p.parent = r;
    }
    return root;
}

/**
 * 右旋, 实际是通过修改节点的父与子指针来实现
 */
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
                                               TreeNode<K,V> p) {
    // l: p 的左孩子
    // pp: p 的父节点
    // lr: p 的左孩子的右孩子
    TreeNode<K,V> l, pp, lr;
    if (p != null && (l = p.left) != null) {
        if ((lr = p.left = l.right) != null)
            lr.parent = p;
        if ((pp = l.parent = p.parent) == null)
            (root = l).red = false;
        else if (pp.right == p)
            pp.right = l;
        else
            pp.left = l;
        l.right = p;
        p.parent = l;
    }
    return root;
}

moveRootToFront

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 红黑树经过旋转后有可能修改根节点, 该方法把数组索引位置指向新根节点, 并修改对应的前后节点
 * tab: 存储数组
 * root: 根节点
 */
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
    int n;
    if (root != null && tab != null && (n = tab.length) > 0) {
        int index = (n - 1) & root.hash;
        TreeNode<K,V> first = (TreeNode<K,V>)tab[index];

        // 索引位置不是根节点
        if (root != first) {
            Node<K,V> rn;
            tab[index] = root;
            TreeNode<K,V> rp = root.prev;

            // 既然重置了根节点, 那么双向链表的头结点就只能是新根节点
            // 所以需要对树的双向链表进行重置了
            // 把根节点前后节点进行连接, 同时根节点 next 指向原来头节点
            // 假设原来的双向链表结构是: A<=>B<=>C<=>D, 其中 C 为新根节点
            // 那么先将 C 前后节点 B D 连接: C, A<=>B<=>D
            // 然后 C 和原来头结点 A 连接: C<=>A<=>B<=>D
            if ((rn = root.next) != null)
                ((TreeNode<K,V>)rn).prev = rp;
            if (rp != null)
                rp.next = rn;
            if (first != null)
                first.prev = root;
            root.next = first;
            root.prev = null;
        }
        assert checkInvariants(root);
    }
}

经过上面的分析我们就可以得出 HashMap 对于树节点插入的大概过程了

  1. 从根节点开始遍历, 比较哈希值, 小于就向左遍历, 大于就向右遍历, 等于就返回节点;
  2. 遍历到最后把新节点插入, 这时候要看新节点是位于祖父节点的左子树还是右子树, 还要看父叔节点颜色;
  3. 新节点是祖父左子树, 并且红父红叔, 那么只要修改颜色即可;
  4. 新节点是祖父左子树, 并且红父黑叔, 这时如果是位于父节点的右子树, 需要先左旋, 然后统一右旋和修改颜色;
  5. 新节点是祖父右子树, 并且红父红叔, 那么同样只修改颜色即可;
  6. 新节点是祖父右子树, 并且红父黑叔, 这时如果是位于父节点的左子树, 需要先右旋, 然后统一左旋和修改颜色.

篇幅原因, 关于树的另一个方法 treeifyBin() 就留到下一 part 再来讲.

如果有疑问欢迎来 Issues 探讨